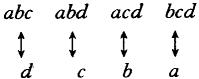教学目标
(1)使学生正确理解组合的意义,正确区分排列、组合问题;
(2)使学生掌握组合数的计算公式、组合数的性质用组合数与排列数之间的关系;
(3)通过学习组合知识,让学生掌握类比的学习方法,并提高学生分析问题和解决问题的能力;
(4)通过对排列、组合问题求解与剖析,培养学生学习兴趣和思维深刻性,学生具有严谨的学习态度。
教学建议
一、知识结构
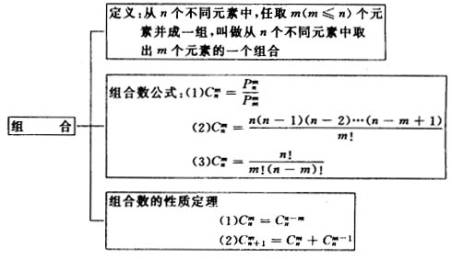
二、重点难点分析
本小节的重点是组合的定义、组合数及组合数的公式,组合数的性质。难点是解组合的应用题。突破重点、难点的关键是对加法原理与乘法原理的掌握和应用,并将这两个原理的基本思想贯穿在解决组合应用题当中。
组合与组合数,也有上面类似的关系。从n个不同元素中任取m(m≤n)个元素并成一组,叫做从n个不同元素中任取m个元素的一个组合。所有这些不同的组合的个数叫做组合数。从集合的角度看,从n个元素的有限集中取出m个组成的一个集合(无序集),相当于一个组合,而这种集合的个数,就是相应的组合数。
解排列组合应用题时主要应抓住是排列问题还是组合问题,其次要搞清需要分类,还是需要分步.切记:排组分清(有序排列、无序组合),加乘明确(分类为加、分步为乘).
三、教法设计
1.对于基础较好的学生,建议把排列与组合的概念进行对比的进行学习,这样有利于搞请这两组概念的区别与联系.
2.学生与老师可以合编一些排列组合问题,如“45人中选出5人当班干部有多少种选法?”与“45人中选出5人分别担任班长、副班长、体委、学委、生委有多少种选法?”这是两个相近问题,同学们会根据自己身边的实际可以编出各种各样的具有特色的问题,教师要引导学生辨认哪个是排列问题,哪个是组合问题.这样既调动了学生学习的积极性,又在编题辨题中澄清了概念.
为了理解排列与组合的概念,建议大家学会画排列与组合的树图.如,从a,b,c,d 4个元素中取出3个元素的排列树图与组合树图分别为:
排列树图 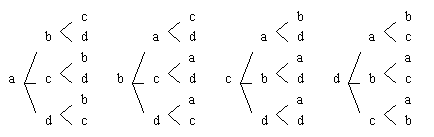
由排列树图得到,从a,b,c,d 取出3个元素的所有排列有24个,它们分别是:abc,abd,acb.abd,adc,adb,bac,bad,bca,bcd,bda,bdc.……dca,dcb.
组合树图
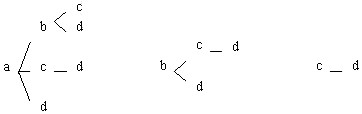
由组合树图可得,从a,b,c,d中取出3个元素的组合有4个,它们是(abc),(abd),(acd),(bcd).
从以上两组树图清楚的告诉我们,排列树图是对称的,组合图式不是对称的,之所以排列树图具有对称性,是因为对于a,b,c,d四个字母哪一个都有在第一位的机会,哪一个都有在第二位的机会,哪一个都有在第三位的机会,而组合只考虑字母不考虑顺序,为实现无顺序的要求,我们可以限定a,b,c,d的顺序是从前至后,固定了死顺序等于无顺序,这样组合就有了自己的树图.
学会画组合树图,不仅有利于理解排列与组合的概念,还有助于推导组合数的计算公式.
3.排列组合的应用问题,教师应从简单问题问题入手,逐步到有一个附加条件的单纯排列问题或组合问题,最后在设及排列与组合的综合问题.
对于每一道题目,教师必须先让学生独立思考,在进行全班讨论,对于学生的每一种解法,教师要先让学生判断正误,在给予点播.对于排列、组合应用问题的解决我们提倡一题多解,这样有利于培养学生的分析问题解决问题的能力,在学生的多种解法基础上教师要引导学生选择最佳方案,总结解题规律.对于学生解题中的常见错误,教师一定要讲明道理,认真分析错误原因,使学生在是非的判断得以提高.
4.两个性质定理教学时,对定理1,可以用下例来说明:从4个不同的元素a,b,c,d里每次取出3个元素的组合及每次取出1个元素的组合分别是