教学目标
（1）掌握复数的有关概念，如虚数、纯虚数、复数的实部与虚部、两复数相等、复平面、实轴、虚轴、共轭复数、共轭虚数的概念。
（2）正确对复数进行分类，掌握数集之间的从属关系；
（3）理解复数的几何意义，初步掌握复数集C和复平面内所有的点所成的集合之间的一一对应关系。
（4）培养学生数形结合的数学思想，训练学生条理的逻辑思维能力．
教学建议
（一）教材分析
1、知识结构
本节首先介绍了复数的有关概念，然后指出复数相等的充要条件，接着介绍了有关复数的几何表示，最后指出了有关共轭复数的概念．
2、重点、难点分析
（1）正确复数的实部与虚部
对于复数 
，实部是 
，虚部是 
．注意在说复数 
时，一定有 
，否则，不能说实部是 
，虚部是 
,复数的实部和虚部都是实数。
说明：对于复数的定义，特别要抓住 
这一标准形式以及 
是实数这一概念，这对于解有关复数的问题将有很大的帮助。
（2）正确地对复数进行分类，弄清数集之间的关系
分类要求不重复、不遗漏，同一级分类标准要统一。根据上述原则，复数集的分类如下：
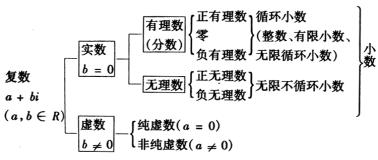
注意分清复数分类中的界限：
①设 
，则 
为实数 
② 
为虚数 
③ 
且 
。
④ 
为纯虚数 
且 
（3）不能乱用复数相等的条件解题．用复数相等的条件要注意：
①化为复数的标准形式 
②实部、虚部中的字母为实数，即 
（4）在讲复数集与复平面内所有点所成的集合一一对应时，要注意：
①任何一个复数 
都可以由一个有序实数对( 
)唯一确定．这就是说，复数的实质是有序实数对．一些书上就是把实数对( 
)叫做复数的．
②复数 
用复平面内的点Z( 
)表示．复平面内的点Z的坐标是( 
)，而不是(
