一、教学目标
1.理解平行线的性质与平行线的判定是相反的问题,掌握平行线的性质.
2.会用平行线的性质进行推理和计算.
3.通过平行线性质定理的推导,培养学生观察分析和进行简单的逻辑推理的能力.
4.通过学习平行线的性质与判定的联系与区别,让学生懂得事物是普遍联系又相互区别的辩证唯物主义思想.
二、学法引导
1.教师教法:采用尝试指导、引导发现法,充分发挥学生的主体作用,体现民主意识和开放意识.
2.学生学法:在教师的指导下,积极思维,主动发现,认真研究.
三、重点·难点解决办法
(一)重点
平行线的性质公理及平行线性质定理的推导.
(二)难点
平行线性质与判定的区别及推导过程.
(三)解决办法
1.通过教师创设情境,学生积极思维,解决重点.
2.通过学生自己推理及教师指导,解决难点.
3.通过学生讨论,归纳小结.
四、课时安排
1课时
五、教具学具准备
投影仪、三角板、自制投影片.
六、师生互动活动设计
1.通过引例创设情境,引入课题.
2.通过教师指导,学生积极思考,主动学习,练习巩固,完成新授.
3.通过学生讨论,完成课堂小结.
七、教学步骤
(一)明确目标
掌握和运用平行线的性质,进行推理和计算,进一步培养学生的逻辑推理能力.
(二)整体感知
以情境创设导入新课,以教师引导,学生讨论归纳新知,以变式练习巩固新知.
(三)教学过程
创设情境,复习导入
师:上节课我们学习了平行线的判定,回忆所学内容看下面的问题(出示投影片1).
1.如图1, 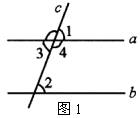
(1)∵![]() (已知),∴
(已知),∴![]() ( ).
( ).
(2)∵![]() (已知),∴
(已知),∴![]() ( ).
( ).
(3)∵![]() (已知),∴
(已知),∴![]() ( ).
( ).
2.如图2,(1)已知![]() ,则
,则![]() 与
与![]() 有什么关系?为什么?
有什么关系?为什么?
(2)已知![]() ,则
,则![]() 与
与![]() 有什么关系?为什么?
有什么关系?为什么?
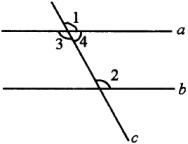
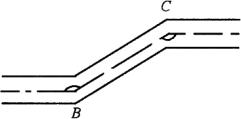
图2 图3
3.如图3,一条公路两次拐弯后,和原来的方向相同,第一次拐的角![]() 是
是![]() ,第二次拐的角
,第二次拐的角![]() 是多少度?
是多少度?
学生活动:学生口答第1、2题.
师:第3题是一个实际问题,要给出![]() 的度数,就需要我们研究与判定相反的问题,即已知两条直线平行,同位角、内错角、同旁内角有什么关系,也就是平行线的性质.板书课题:
的度数,就需要我们研究与判定相反的问题,即已知两条直线平行,同位角、内错角、同旁内角有什么关系,也就是平行线的性质.板书课题:
[板书]2.6 平行线的性质
【教法说明】通过第1题,对上节所学判定定理进行复习,第2题为性质定理的推导做好铺垫,通过第3题的实际问题,引入新课,学生急于解决这个问题,需要学习新知识,从而激发学生学习新知识的积极性和主动性,同时让学生感知到数学知识来源于生活,又服务于生活.
探究新知,讲授新课
师:我们都知道平行线的画法,请同学们画出直线![]() 的平行线
的平行线![]() ,结合画图过程思考画出的平行线,找一对同位角看它们的关系是怎样的?
,结合画图过程思考画出的平行线,找一对同位角看它们的关系是怎样的?
学生活动:学生在练习本上画图并思考.
学生画图的同时教师在黑板上画出图形(见图4),当同学们思考时,教师有意识地重复演示过程.
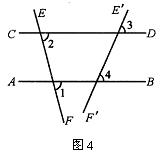
【教法说明】让同学们动手、动脑、观察思考,使学生养成自己发现问题得出规律的习惯.
学生活动:学生能够在完成作图后,迅速地答出:这对同位角相等.
提出问题:是不是每一对同位角都相等呢?请同学们任画一条直线![]() ,使它截平行线
,使它截平行线![]() 与
与![]() ,得同位角
,得同位角![]() 、
、![]() ,利用量角器量一下;
,利用量角器量一下;![]() 与
与![]() 有什么关系?
有什么关系?
学生活动:学生按老师的要求画出图形,并进行度量,回答出不论怎样画截线,所得的同位角都相等.
根据学生的回答,教师肯定结论.
师:两条直线被第三条直线所截,如果这两条直线平行,那么同位角相等.我们把平行线的这个性质作为公理.
[板书]两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
【教法说明】在教师提出问题的条件下,学生自己动手,实际操作,进行度量,在有了大量感性认识的基础上,动脑分析总结出结论,不仅充分发挥学生主体作用,而且培养了学生分析问题的能力.
提出问题:请同学们观察图5的图形,两条平行线被第三条直线所截,同位角是相等的,那么内错角、同旁内角有什么关系呢?
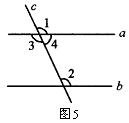
学生活动:学生观察分析思考,会很容易地答出内错角相等,同分内角互补.
师:教师继续提问,你能论述为什么内错角相等,同旁内角互补吗?同学们可以讨论一下.
学生活动:学生们思考,并相互讨论后,有的同学举手回答.
【教法说明】在前面复习引入的第2题的基础上,通过学生的观察、分析、讨论,此时学生已能够进行推理,在这里教师不必包办代替,要充分调动学生的主动性和积极性,进而培养学生分析问题的能力