一、教学目标
1.了解立方根和开立方的概念；
2.会用根号表示一个数的立方根，掌握开立方运算；
3.培养学生用类比的思想求立方根的运算能力；
4.由立方与立方根的教学，渗透数学的转化思想；
5.通过立方根符号的引入体验数学的简洁美.
二、教学重点和难点
教学重点：立方根的概念与性质．
教学难点：会求某些数的立方根．
三、教学方法
启发式，讲练结合
四、教学手段
幻灯片．
五、教学过程
(一)复习提问
请同学们回忆一下，平方根我们是如何定义的？平方根有哪些性质？
在同学们回答后，启发学生是否可试着给数的立方根下个定义．
1．立方根的概念：
如果一个数的立方等于a，这个数就叫做a的立方根．(也称数a的三次方根)
用数学式表示为：
若x3=a，则x叫做a的立方根，或称x叫做a的三次方根．
2．立方根的表示方法：
类似于平方根德表示方法，数a的立方根我们用符号
来表示.读作“三次根号下a”，其中a叫做被开方数，3叫做根指数，注意，在前面我们学习平方根的表示方法说过当根指数为2时可以省略不写，现在是立方根了，这个根指数3是绝对不可省的，否则就会与平方根混淆了，例如
表示125的立方根，而
则表示125的算术平方根.
练习：用根号表示下列各数的立方根：
3．开立方概念：
求一个数的立方根的运算，叫做开立方．
4．开立方运算与立方运算互为逆运算．
因此，我们可以根据立方运算来求一些数的立方根．
例1． 求下列各数的立方根：
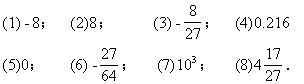
解：(1)∵(-2)3=-8，
(2)∵23=8，
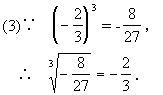
(4)∵ (0.6)3=0.216，
(5)∵03=0，
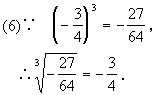
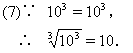
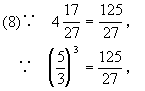
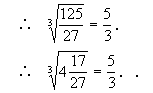
下面我们思考这样一个问题：一个正数有几个平方根？负数有没有平方根？一个正数有几个立方根？负数有没有立方根？请学生来回答这个问题．由前面刚刚做过的题我们不难看出像8、0.126、103、
这样的正数，有一个正的立方根；像-8、
、
这样的负数有一个负的立方根；0的立方根是0．由此我们得了立方根的性质．
5．立方根的性质：
(1)正数有一个正的立方根．
(2)负数有一个负的立方根．
(3)0的立方根是0．
这里我们不妨与平方根的性质做个比较，平方根中，正数有两个平方根，它们互为相反数，正数只有一个正的立方根；在平方根中负数是没有平方根的，而负数有一个负的立方根；平方根与立方根唯一相同之处是0的平方根，立方根都是它本身．
