教学目标:
1、知识目标:
(1)掌握勾股定理;
(2)学会利用勾股定理进行计算、证明与作图;
(3)了解有关勾股定理的历史.
2、能力目标:
(1)在定理的证明中培养学生的拼图能力;
(2)通过问题的解决,提高学生的运算能力
3、情感目标:
(1)通过自主学习的发展体验获取数学知识的感受;
(2)通过有关勾股定理的历史讲解,对学生进行德育教育.
教学重点:勾股定理及其应用
教学难点:通过有关勾股定理的历史讲解,对学生进行德育教育
教学用具:直尺,微机
教学方法:以学生为主体的讨论探索法
教学过程:
1、新课背景知识复习
(1)三角形的三边关系
(2)问题:(投影显示)
直角三角形的三边关系,除了满足一般关系外,还有另外的特殊关系吗?
2、定理的获得
让学生用文字语言将上述问题表述出来.
勾股定理:直角三角形两直角边![]() 的平方和等于斜边
的平方和等于斜边![]() 的平方
的平方
强调说明:
(1)勾――最短的边、股――较长的直角边、弦――斜边
(2)学生根据上述学习,提出自己的问题(待定)
学习完一个重要知识点,给学生留有一定的时间和机会,提出问题,然后大家共同分析讨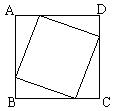 论.
论.
3、定理的证明方法
方法一:将四个全等的直角三角形拼成如图1所示的正方形.
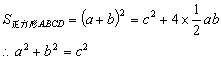
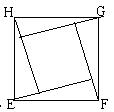 方法二:将四个全等的直角三角形拼成如图2所示的正方形,
方法二:将四个全等的直角三角形拼成如图2所示的正方形,
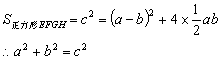
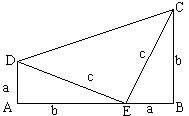
方法三:“总统”法.如图所示将两个直角三角形拼成直角梯形
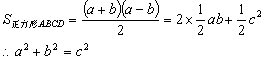
以上证明方法都由学生先分组讨论获得,教师只做指导.最后总结说明
4、定理与逆定理的应用
例1 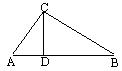 已知:如图,在△ABC中,∠ACB=
已知:如图,在△ABC中,∠ACB=![]() ,AB=5cm,BC=3cm,CD⊥AB于D,求CD的长.
,AB=5cm,BC=3cm,CD⊥AB于D,求CD的长.
解:∵△ABC是直角三角形,AB=5,BC=3,由勾股定理有
![]()
∴![]() ∠2=∠C
∠2=∠C
又![]()
∴![]()
∴CD的长是2.4cm
例2 如图,△ABC中,AB=AC,∠BAC=![]() ,D是BC上任一点,
,D是BC上任一点,
求证:![]()
证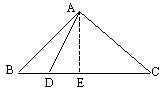 法一:过点A作AE⊥BC于E
法一:过点A作AE⊥BC于E
则在Rt△ADE中,![]()
又∵AB=AC,∠BAC=![]()
∴AE=BE=CE
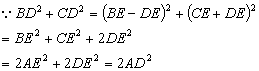
即![]()
证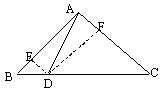 法二:过点D作DE⊥AB于E, DF⊥AC于F
法二:过点D作DE⊥AB于E, DF⊥AC于F
则DE∥AC,DF∥AB
又∵AB=AC,∠BAC=![]()
∴EB=ED,FD=FC=AE
在Rt△EBD和Rt△FDC中
![]()
![]()
在Rt△AED中,![]()
∴![]()